分数の攻略_6

◎分数を使った大きさの表し方
今回は、分数を使った大きさの表し方を学習します。
では、まずは次のクイズに挑戦してみましょう。
1円を3人で分けることはできませんね。では、1Lの牛乳を3人で分けることはできますか?
3つのコップに上手に分ければ平等に分けることができますね。

この1人分の量(りょう)のことを分数を使って表すとどうなるでしょう?
1Lを「3つに分けたうちの1つ分」なので、
$\large\frac{1}{3}$L
と書いて(3ぶんの1リットル)と読みます。
分数の後ろに L という単位がついているところが、今までの分数と違っていますね。
今まで学んだ分数には、そのような単位は付いていませんでしたけど、
今回は L(リットル)という単位がついていて、
これは1Lの $\large\frac{1}{3}$ (3等分したうちの1つ分)の量であることを表しています。
そして、2人分の量(上の図のコップ2はい分の量)のことは、
$\large\frac{2}{3}$L
と書いて、(3ぶんの2リットル)と読みます。
では、3人分の量のことは、どう書きますか?
$\large\frac{3}{3}$L
ですね。でも、これはもとの量 1L のことですから、
$\large\frac{3}{3}$L と 1L は同じ ということになります。
ですから、
$\large\frac{3}{3}$L=1L
と書くことができますね。
このことは、1Lの牛乳を分けた時だけでなく、1mのテープを分けた時も、単位が違うだけで同じ書き方をします。
1mのテープの$\large\frac{1}{3}$(3等分したうちの1つ分)の長さのことを、
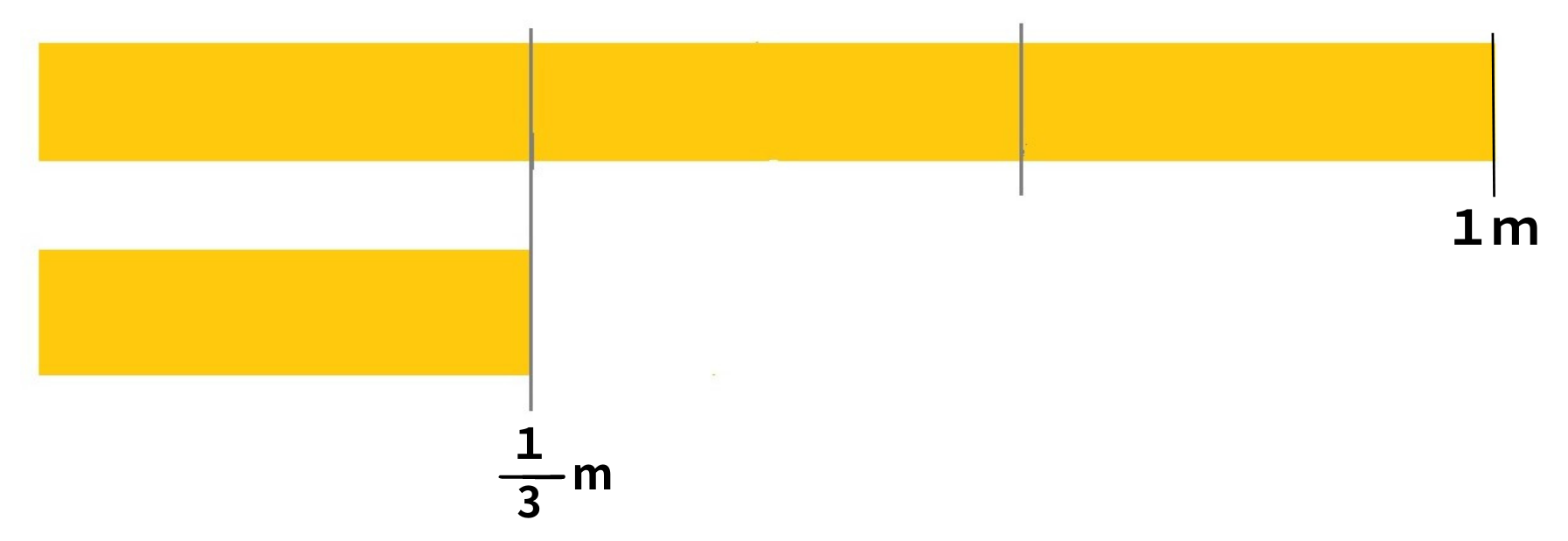
$\large\frac{1}{3}$m
と書いて、(3ぶんの1メートル)と読み、
1gの重さの$\large\frac{1}{3}$(3等分したうちの1つ分)は
$\large\frac{1}{3}$g
と書いて、(3ぶんの1グラム)と読みます。
そして、それぞれの3つ分は、やはり
$\large\frac{3}{3}$m=1m
$\large\frac{3}{3}$g=1g
と書くことができますね。
では今度は、L,m、gなどの単位がない分数ではどうでしょう?
数直線を使って考えましょう。
数直線については、3年下の教科書にくわしく説明されていますから、
よくわかっていない場合は、まずそちらで確認してみてね。
$\large\frac{1}{5}$
は(5等分したうちの1つ分)のことですから、
それが5つだと
$\large\frac{5}{5}$
と書くことが出来ますし、

数直線をみると、それは1のことですから、やはり、
$\large\frac{5}{5}$=1
と書くことができます。
では、
$\large\frac{7}{7}$(7等分した内の7つ分)はどうでしょう?

やはり
$\large\frac{7}{7}$=1
になりますね。
ですから、式で書くと次のようになります。
1=$\large\frac{2}{2}$=$\large\frac{3}{3}$=$\large\frac{4}{4}$=$\large\frac{5}{5}$=$\large\frac{6}{6}$=$\large\frac{7}{7}$=$\large\frac{8}{8}$=・・・・・
このように、分母と分子が同じ分数は、すべて1になります。
(重要ポイント)
※分数も、小数と同じように量や長さ、重さなどの大きさを表すことができる
※分母の数と分子の数が同じだと、その数はみんな 1と同じ になります
今回は、分数も、小数と同じように量や長さ、重さなどの大きさを表すことができるということを学びました。
復習として、1Lの牛乳を5人で分けた内の3人分や、4人分のことを分数で表すとどうなるか、
余裕があれば(mとcmの換算が簡単にできる子の場合)、1mを100等分した内の1つ分の長さが何cmになるかなどを考えさせてみると良いと思います。
最後まで読んでくださり、ありがとうございます。いつものように、ご意見・ご感想・シェアなどをいただけるとありがたいです。今後ともどうぞよろしくお願いいたします。