分数の攻略_9

◎帯分数を仮分数になおす方法
前回では、
「仮分数を帯分数になおす方法」を学びましたが、
今回は、ぎゃくの「帯分数を仮分数になおす方法」を身につけましょう。
まず、
2$\large\frac{2}{5}$
を仮分数になおす方法を考えます。
2$\large\frac{2}{5}$=2+$\large\frac{2}{5}$
ということですから、まず整数の2を分数になおすことを考えます。
分数部分の $\large\frac{2}{5}$ に合わせて、計算しやすいように、
分母が5の分数を使いましょう。
1は、$\large\frac{1}{5}$ が5こ分のことなので、
1=$\large\frac{5}{5}$
2は、$\large\frac{1}{5}$ が10こ分ということになり、
2=$\large\frac{10}{5}$
となります。
分数部分の $\large\frac{2}{5}$ というのは、
$\large\frac{1}{5}$ が2こ ということですから、
$\large\frac{10}{5}$ と $\large\frac{2}{5}$
になりますね。
全部で $\large\frac{1}{5}$ がいくつになるかを計算すると
整数部分の2は、$\large\frac{5}{5}$ が2つなので、10こ
分数部分の $\large\frac{2}{5}$ は、2こ
式に書くと
5×2+2=12
ですね。
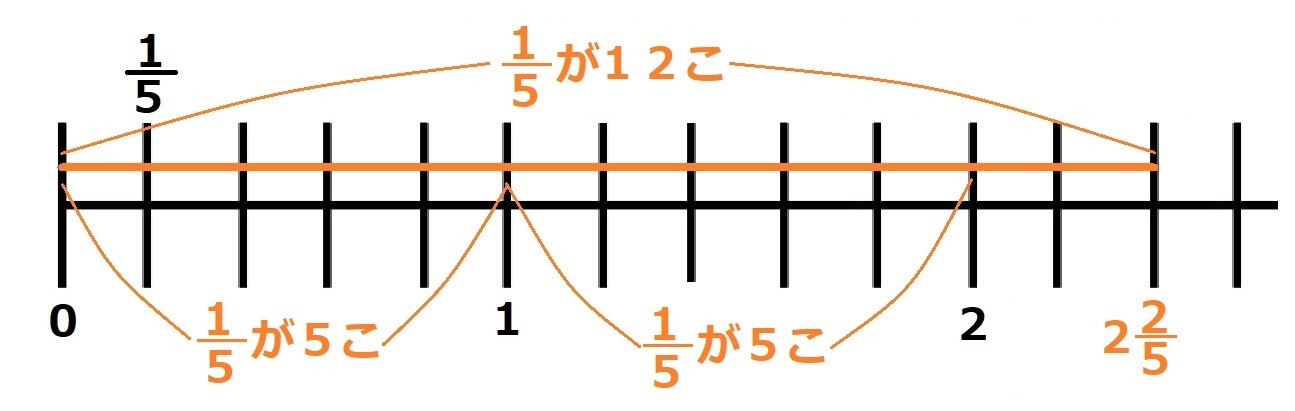
$\large\frac{1}{5}$ が12こ ということなので、
仮分数で表すと
$\large\frac{12}{5}$
となります。
数直線を見ながら確認してみましょう。
ここで、分数の基本をおさらいしておきます。
$\large\frac{3}{4}$
を例にすると、
この分数の意味は
「4つに分けた内の3つ分」
ということでしたね。
ただ、何を4つに分けた内の3つ分なのかをしっかりと理解しておくことが大切です。
たとえば、
・1本のテープを4つに分けた内の3つ分なら、「テープの $\large\frac{3}{4}$ 」
・8個のキャンディーを4つに分けた内の3つ分なら、「8個の $\large\frac{3}{4}$ 」
・1mを4つに分けた内の3つ分なら、「1mの $\large\frac{3}{4}$ 」
というように、「何の $\large\frac{3}{4}$ 」なのか、ということを分かっておく必要があります。
お店に入って、「 $\large\frac{3}{4}$ ください」と言っても、
「何の $\large\frac{3}{4}$ ですか?」とたずねられることでしょう。
「ケーキを4人で分けることになっていて、先に来た3人分をもらいたい」ということでしたら
「このホールケーキの $\large\frac{3}{4}$ をください」
という言い方をしないと通じませんよね。
この基本はとても大切なので、しっかりと頭に入れておきましょう。
その上で、次は分数の大きさ比べを学びます。
◎分数の大きさ比べ
$\large\frac{11}{5}$ と 2$\large\frac{2}{5}$ は、どちらが大きいでしょうか?
でも、分数の大きさは、
もとの大きさが変われば、同じ分数でも大きさが違う
と、前に学びましたね。覚えてくれていますか。
たとえば、パンダの体重(80kg)の $\large\frac{1}{4}$
と、ペンギンの体重(20kg)の $\large\frac{1}{4}$
では、同じ
$\large\frac{1}{4}$
でも、パンダの体重の $\large\frac{1}{4}$ の方が大きいですよね。
ですから、
すぐ上にも書きましたが、分数の大きさを考える時は、
「何の $\large\frac{1}{4}$ 」なのかを理解しておく必要があります。
ここで1つ、大切なお約束がありますので、ぜひ覚えておいてください。
それは、分数を使う時
「パンダの体重の $\large\frac{1}{4}$ 」とか、
「身長の $\large\frac{1}{8}$ 」、のような
「〇〇の」という前置きの言葉が付いていない分数
つまり
$\large\frac{1}{4}$ とか $\large\frac{3}{5}$
のように、分数だけが書いてあるときは、
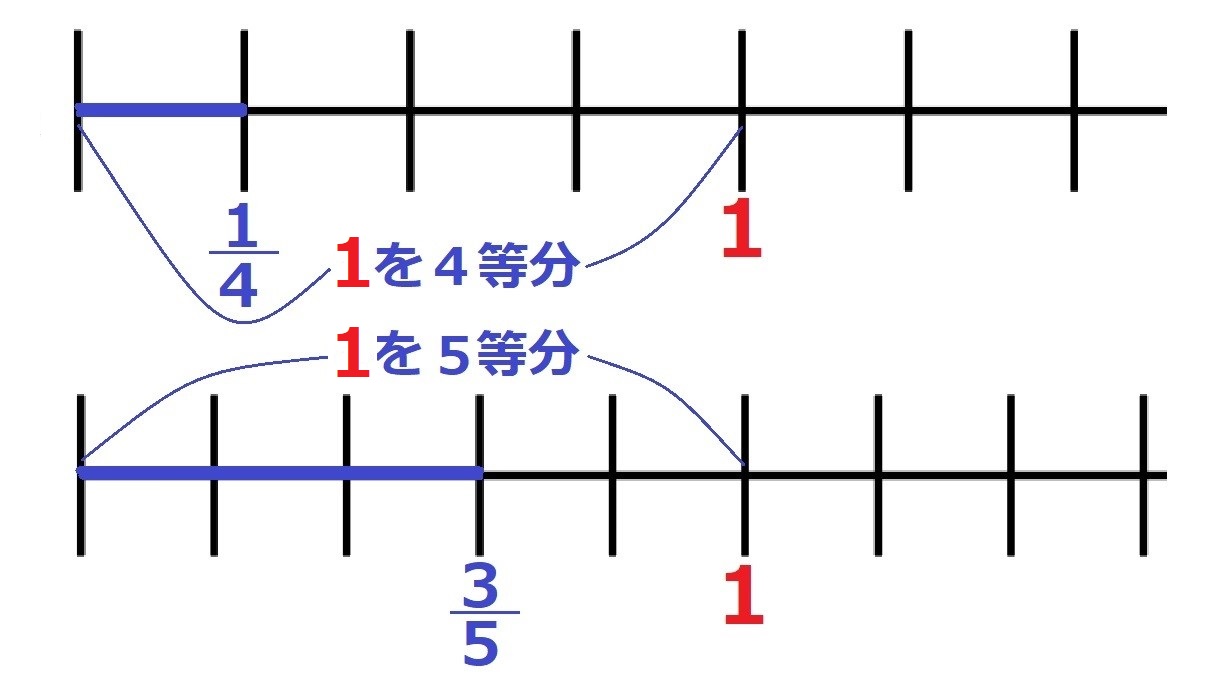
「1の $\large\frac{1}{4}$ 」、「1の $\large\frac{3}{5}$ 」という意味になる
という約束です。
数直線で書くと、
こういうことですね。
また、
$\large\frac{1}{2}$Lのように単位を付けて書いてあるときは、1Lの $\large\frac{1}{2}$
$\large\frac{1}{4}$mと書いてあるときは、1mの $\large\frac{1}{4}$
$\large\frac{2}{5}$kgと書いてあるときは、1kgの $\large\frac{2}{5}$
という意味になります。
このように、1という数は、もと(基準)の大きさの数として、
これからもよく使われますので、覚えておいてください。
さて、問題に戻りましょう。
$\large\frac{11}{5}$ と 2$\large\frac{2}{5}$ は、どちらが大きいでしょうか?
という問題でしたね。
これは、分数の前に「〇〇の」と書いていませんので、
「1の $\large\frac{11}{5}$ 」(1を5等分したものの11こ分)
と
「1の 2$\large\frac{2}{5}$ 」{2+(1を5等分したものの2こ分)}
の大きさを比べるという意味になります。
2$\large\frac{2}{5}$ (帯分数)の方は、大きさのめやすは、すぐ分かりますね。
そう、2よりも $\large\frac{2}{5}$ だけ大きい数となります。
$\large\frac{11}{5}$ (仮分数)の方は、その大きさがこのままでは分かりにくいので、
帯分数になおして比べてみましょう。
$\large\frac{11}{5}$
を帯分数になおすには、次の計算をします。
11÷5=2...1
(11の中に5は2こあり、あまりは1)なので、
整数部分は 2
分数部分は $\large\frac{1}{5}$
ということで
$\large\frac{11}{5}$ = 2$\large\frac{1}{5}$
となるので、
2$\large\frac{2}{5}$ の方が大きいことが分かります。
このことを <(不等号) を使って、下のように書き表します。
$\large\frac{11}{5}$ < 2$\large\frac{2}{5}$
また、両方を仮分数にそろえても、大きさを比べることができますので、
その方法でも考えてみましょう。
2$\large\frac{2}{5}$
を仮分数になおすには、
2$\large\frac{2}{5}$
は、$\large\frac{1}{5}$ が何こ分になるかを考えれば良いので、
2$\large\frac{2}{5}$ の整数部分と分数部分に分けて考えます。
整数部分の 2 については、
1が、$\large\frac{1}{5}$ の5こ分なので、
2は、$\large\frac{1}{5}$ の10こ分になります。
分数部分の $\large\frac{2}{5}$ については
$\large\frac{1}{5}$ が2こ分ということですね。
ですから、両方で、$\large\frac{1}{5}$ が12こ分ということになるので、
2$\large\frac{2}{5}$ = $\large\frac{12}{5}$
となります。ということから、
$\large\frac{11}{5}$ と比べると、やはり、2$\large\frac{2}{5}$ の方が大きいことが分かるので、
$\large\frac{11}{5}$ < 2$\large\frac{2}{5}$
となります。
もう一つ、別の方法で比べてみましょう。
それは、数直線を使う方法です。
下の図のように数直線に仮分数と帯分数を両方書いて比べてみます。
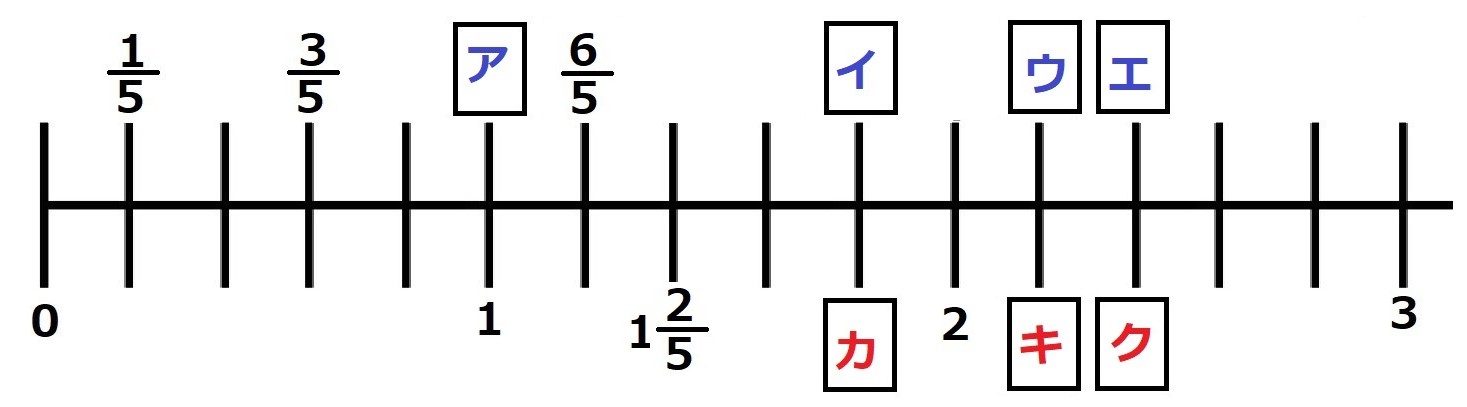
$\large\frac{11}{5}$
は、上の数直線のア、イ、ウ、エのどれになりますか
そう、ウですね。
もし分からなければ、分数の意味から復習しましょう。
分数の意味は、たとえば、
$\large\frac{3}{5}$
は、1を5等分したものの3つ分
ということでしたね。
だから、
$\large\frac{11}{5}$
は、1を5等分したものの11こ分
ということになります。
数直線を見ると
0から1までの間を5等分した線が書いてありますね。
ですから、その1つ目が $\large\frac{1}{5}$ 、3つめが $\large\frac{3}{5}$
となります。
そう考えると、
アは、1を5等分したものの5つ分だから、$\large\frac{5}{5}$ になりますね。
同じように、
イは、1を5等分したものの9こ分だから、$\large\frac{9}{5}$ になりますね。
そうすると、
ウとエは、それぞれ $\large\frac{11}{5}$ 、$\large\frac{12}{5}$
になりますね。
次に、
2$\large\frac{2}{5}$
は、カ、キ、クのどれになりますか?
カは2より小さいから、違いますね。
ウは2より $\large\frac{1}{5}$ だけ大きいので、
2$\large\frac{1}{5}$
ですね。
クは2より $\large\frac{1}{5}$ が2こ分だけ大きいですね。
ですから、
2+ $\large\frac{2}{5}$ = 2$\large\frac{2}{5}$
なので、クが正解になります。
このように、数直線で調べても
$\large\frac{11}{5}$ < 2$\large\frac{2}{5}$
であることが分かります。
では、練習問題です。
次の3つの分数を大きい順に書きましょう。
(1) 2$\large\frac{1}{3}$ と $\large\frac{8}{3}$ と 2
(2) $\large\frac{5}{4}$ と 1$\large\frac{2}{4}$ と $\large\frac{7}{4}$
◎分子が1で分母が違う分数の大きさ比べ
では、次の分数の大きさはどちらが大きいか、分かりますか。
$\large\frac{1}{5}$ $\large\frac{1}{6}$
分母の数が違うので、ちょっと分かりにくいかもしれません。
でも、分数の意味を思い出して、考えると分かりますよ。
分母の数と言うのは、いくつに分けたかを表す数でしたね。
$\large\frac{1}{5}$
なら、5等分したものの1つ分
$\large\frac{1}{6}$
なら、6等分したものの1つ分
ということになります。
1つのケーキを
5人で分けた時よりも、
6人で分けた時の方が
1人分は小さくなることを思い浮かべれば、分かりますね。
どちらも、分子が1ということは、1つ分ということなので、
5等分したものより、6等分したものの方が、小さくなりますね。
ですから、
$\large\frac{1}{6}$ < $\large\frac{1}{5}$
下に、分子が1の時の分数の大きさを数直線で、表していますので、
確認しておきましょう。
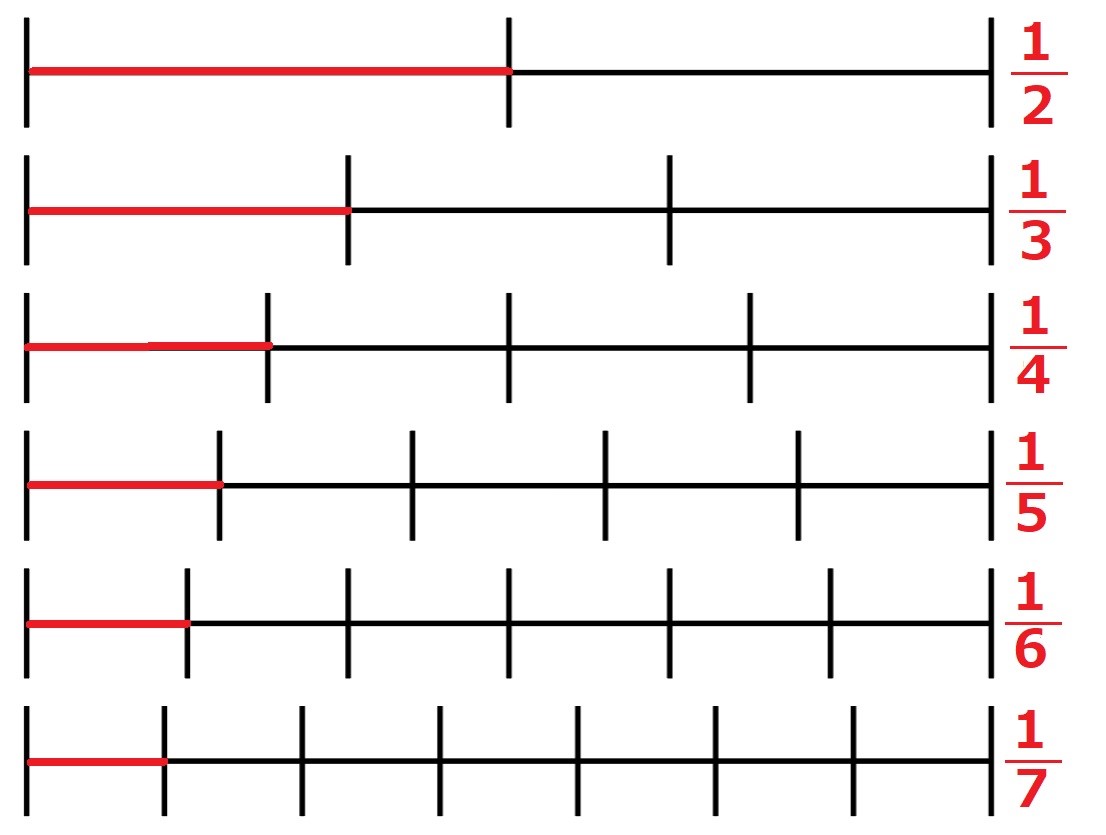
また、以下のリンク先の分数ケーキも、とても分かりやすい作りになっていますので、見ていただくと良いと思います。
分数ケーキ(熊本市教育センター)
今回は、
◎帯分数を仮分数になおす方法
◎分数の大きさ比べ
◎分数の原則として、前置きが無い時は「1を〇等分したもの」と考える
◎分子が1で分母が違う分数の大きさ比べ
について学びました。
この辺りから、分数に苦手意識が芽生えることが多いので、
「分数の攻略_8」「分数の攻略_9」をしっかり理解した上で、
以下の確認問題に、自信がつくまで取り組ませてあげてください(足し算・引き算の手前まで)。
・4年の分数の確認問題
分数の大きさとたし算,ひき算
4年分数
最後まで読んでくださり、ありがとうございました。
以下のボタンによるシェアや、コメント欄・お問い合わせからのご意見・ご感想などをいただけると嬉しいです。今後ともどうぞよろしくお願いいたします。