分数の攻略_4

◎分数の読み方、書き方、定義

まずは小学２年生レベルから

３０cmほどの紙テープ（A4の紙を１ｃｍ幅に切ったものでもＯＫ）２本を準備して、

半分の長さにするにはどうしたらいい？
と尋ね、１本をこうして半分に折り、上の図のように並べます。

「この、同じ大きさに２つに分けた　１つ分」のことを
もとの大きさの二分の一（にぶんのいち）と言って、

　　　$\large\frac{1}{2}$

と書くんだよ、と説明し、
子どもに「二分の一」と言わせましょう。

（補：「２つに分けた　１つ分」のところ、教科書表記に従いましたが、日本語として自然な言い回しは「２つに分けたあとの１つ分」とか「２つに分けたうちの１つ分」になるかと思われますので、しっくりこない方はそのように言い換えても良いと思います）

そしてノートに

　　　$\large\frac{1}{2}$

　と書きながら、書き順｛1：横バー、2：分母(2)、3：分子(1)｝も教え、
「にぶんのいち」　と言わせながら３回書かせます。

半分にしたテープを指さしながら、
「もとの大きさの　$\large\frac{1}{2}$　というのは、
同じ大きさに２つに分けた　１つ分のこと」
と言って復唱させます。

更に、もう一度半分に折らせます。

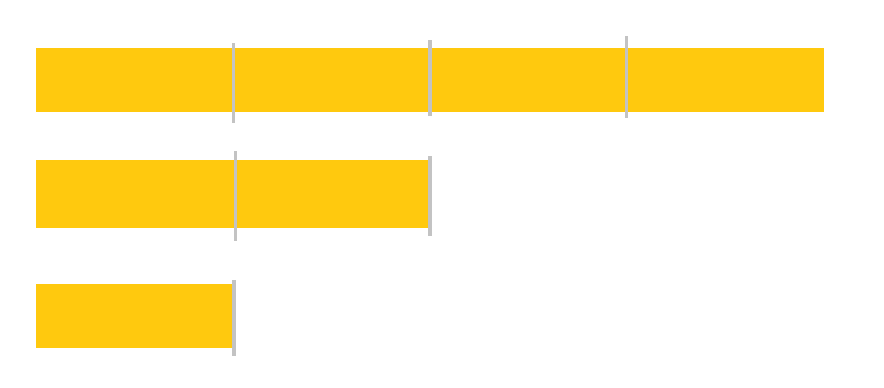
これは、もとの大きさの　半分の　半分の大きさだね。
この大きさは　もとの大きさの（　　　　）といいますか？
と尋ねてみましょう。正解なら、
「正解！」と誉め、
答えに詰まっていたら、テープを広げて見せます。
折り目を利用して、
「同じ大きさに４つに分けた　１つ分の大きさになっているね」と確認し、
この大きさのことを何と言いますか？
と尋ねてみましょう。
たぶん、　$\large\frac{1}{4}$　と答えますから、「そうだね、いいね」と認めた後、
正確に言うと「もとの大きさの　$\large\frac{1}{4}$　」と言った方が良いよ、と補足しておきます。

この「もとの大きさの」という言葉を付けるのは、
面倒ではありますが、後々割合を学ぶときに生きてきます。

答えに詰まっていたら、
「同じ大きさに２つに分けた　１つ分のことは、もとの大きさの　$\large\frac{1}{2}$　だったね」
だから、
「同じ大きさに４つに分けた　１つ分のことは、もとの大きさの　$\large\frac{1}{4}$　と言うんだよ」
と優しく教えます。

今度は、「４つに分けた　１つ分」と口に出させながら、

ノートに　$\large\frac{1}{4}$　を３回書かせます。

そして、ノートに書いた　$\large\frac{1}{2}$　や　$\large\frac{1}{4}$　の数のことを「分数」と言うことを教えます。

ほかにどんな分数があると思う？　と尋ねてみましょう。

　$\large\frac{1}{10}$　とか　$\large\frac{1}{100}$　という答が返ってくるかもしれません。

いいね！　と言っていっぱい拍手をしてあげましょう。中には

　$\large\frac{2}{3}$　と言う子がいるかもせれません。

「すごい！　こんな風に、いろんな分数がたくさんあるから、これから少しずつ一緒に勉強して行こうね」と言ってハグしてあげましょう。

◎分数を何倍にすると、もとの大きさになるかな？

ここで、もとの大きさの　$\large\frac{1}{4}$　に折ったテープがいくつあると、もとの大きさになるかを尋ねてみましょう。
答えに詰まれば、テープを広げて、４つ分あればもとの大きさになるねと確認し、
更に、もとの大きさの　$\large\frac{1}{2}$　に折ったテープがいくつあると、もとの大きさになるかを尋ねてみます。
答えに詰まれば同様に、テープを広げて、２つ分でもとの大きさになることを確認します。

ここでは、

　$\large\frac{1}{4}$　を４倍にするともとの大きさになり、

　$\large\frac{1}{2}$　を２倍にするともとの大きさになることを、

うっすらと感じられれば充分です。

◎分ける数が増えると、分数の大きさは小さくなる

　$\large\frac{1}{4}$　に折ったテープをさらに半分に折って、ずいぶん小さくなったねとつぶやきながら、この大きさを分数で表せるか、尋ねてみます。
答えに詰まるようなら、テープを広げて、

同じ大きさに８つに分けた１つ分になっていることを確認し、

この大きさを分数で表すと、何と言うか尋ねます。

答えに詰まるようなら、
「同じ大きさに２つに分けた１つ分のことは、もとの大きさの　$\large\frac{1}{2}$　と言って」
「同じ大きさに４つに分けた１つ分のことは、もとの大きさの　$\large\frac{1}{4}$　と言うんだったね」と優しく教え
もとの大きさの　$\large\frac{1}{8}$　という返事を待ちます。

次に、紙テープをもう１枚準備し、

もとの大きさの　$\large\frac{1}{3}$　は、どのくらいの大きさになるかな？
と尋ねながら、折り方を一緒に考えます。

◎もとの大きさが違うと、その分数の大きさは？

次に、もとのテープの大きさが違う場合について学びます。

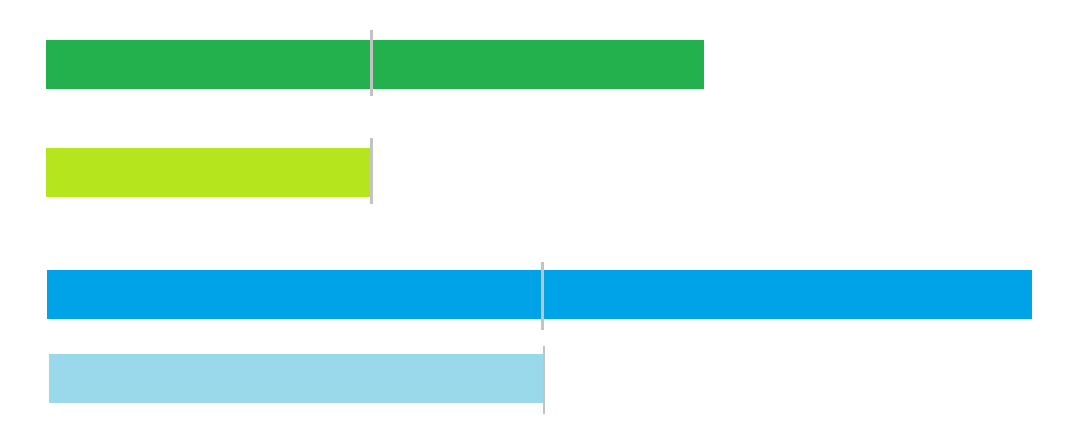
黄緑色のテープは緑色のテープの　$\large\frac{1}{2}$　、
水色のテープは青色のテープの　$\large\frac{1}{2}$　で、

どちらも　$\large\frac{1}{2}$　ですが、
大きさが違っています。

もとの大きさが違うと、　$\large\frac{1}{2}$　の大きさも違いますね。

今度はドーナツとキャンディで比べてみましょう。

ドーナツは１２こあり、キャンディは１８こあります。

それぞれの　$\large\frac{1}{3}$　の数について調べましょう。

ドーナツの数の　$\large\frac{1}{3}$　は（　　）こですね。

答えに戸惑っているようでしたら、横線を引いてみたらどうかな、とヒントを与えてください。

キャンディの数の　$\large\frac{1}{3}$　は（　　）こになりますね。

やはり、もとの数が違うと、　$\large\frac{1}{3}$　の数も違いますね。

以上で、２年生の分数は終わりです。

◎まとめ

今回は、算数的な理解は難しくないと思いますが、

大切なことは、分数の意味を理解して、使いこなせるかどうかです。

「同じ大きさに４つに分けた　１つ分」のことを「もとの大きさの　$\large\frac{1}{4}$　」という

このような定義を丸暗記させる必要はありません。
大人が的確に覚えおいて、それを繰り返し言葉に出してあげれば十分です。

使いこなすために、例えばお風呂に５００mLと２Lのペットボトル、メジャーカップを持って入り、
「５００mlの　$\large\frac{1}{2}$　をメジャーカップに入れてください」
「５００mlの　$\large\frac{1}{5}$　をメジャーカップに入れてください」
などと依頼して、やらせてみると良いかも知れません。

２Lの　$\large\frac{1}{4}$　が、５００mlのペットボトル１本分になることや、
　$\large\frac{1}{4}$　の量の４倍がもとの大きさになることに気づいたりして、楽しめるとおもいます。

「５００mlの　$\large\frac{2}{5}$　がどのくらいになるかな？　　$\large\frac{1}{5}$　の２つ分ということかな」などと、先取り学習も、楽しくできるかもしれません。

こうして、生活の中に分数を取り入れて、分数に親しませ、使いこなせるように導いてあげるのが一番です。

買ってもらったおやつも、「１週間分よ」と言われたときに、
「じゃ、１日に　$\large\frac{1}{7}$　ずつ食べたらいいね」
と自分で言えるようになると良いかと思います。

今日の格言：習ったことはすぐ使う

また、この年代の楽しい時の記憶力は、ずば抜けていますから、そんな時は、
「同じ大きさに３つに分ける」ことを「３等分」
「同じ大きさに４つに分ける」ことを「４等分」
という言い方をするんだよ。と教えると、
「４等分したときの１つ分」
と、より簡単な言葉で理解が進むようになります。

そして最後に、
「分かった」というのは「分かったつもりになっているだけ」です。
理解　ー＞　基礎力　ー＞　応用力　という流れで本物の実力になります。
以下のリンク先の問題（秀逸！　解答付）で、しっかりと自信をつけさせてあげましょう。

「花まるワーク2年下巻」 　　の「単元17　1を分けて」

今回も長文にもかかわらず、最後まで読んでくださりありがとうございました。

何かお気づきの点などございましたら、下部コメント欄やお問い合わせから教えてくださいますようお願いいたします。

分数を苦手とする子どもたちは数えきれないほど大勢います。
その子たちのサポーターも同じ数だけ必要です。
もし、この記事がお役に立てるようでしたら、下のボタンで拡散していただけると嬉しいです。
よろしくお願いします。