◎分数の足し算と引き算
では、まずは質問から。次の計算は正しいでしょうか？
$\large\frac{1}{4}$＋$\large\frac{2}{4}$＝$\large\frac{3}{8}$ ？
（分子どうしを足して１＋２＝３、分母どうしを足して４＋４＝８
という計算をしていますね）
数直線を使って、正しいかどうかを確認してみましょう
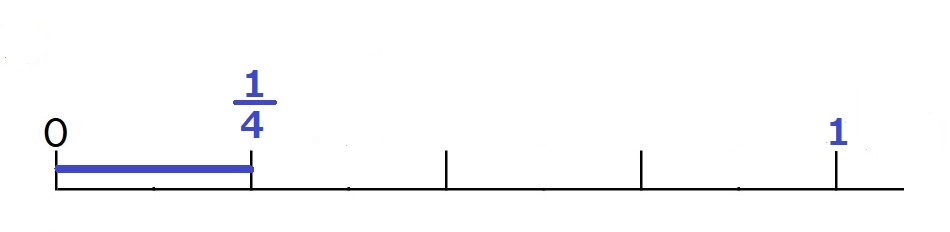$\large\frac{1}{4}$ （青い部分）
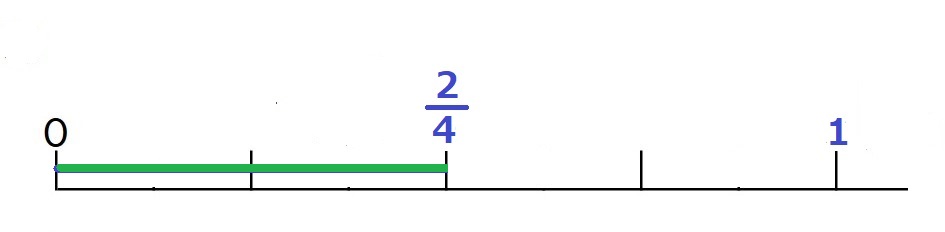$\large\frac{2}{4}$ （緑の部分）
この二つを足した結果は、とうぜん半分以上の大きさになるはずですから、
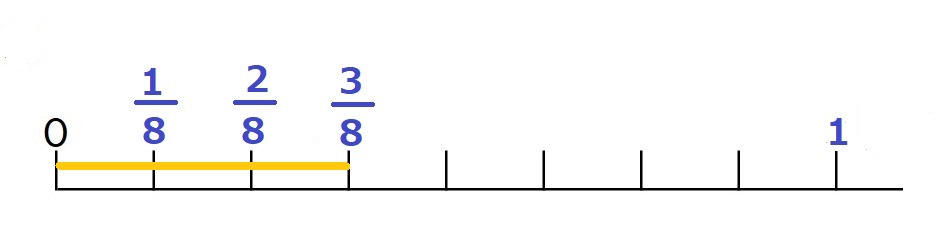$\large\frac{3}{8}$ （黄色の部分）
は、まちがいですね。では、正解は？
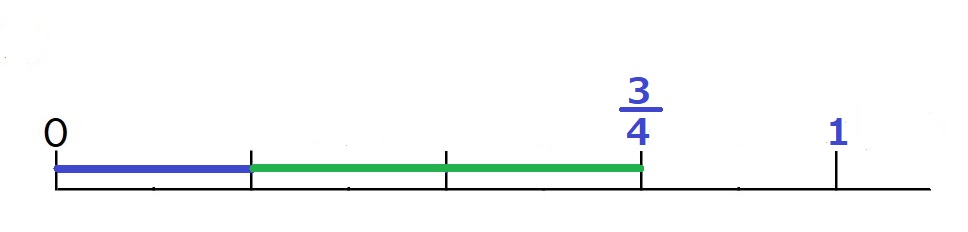$\large\frac{3}{4}$ （青と緑の部分）
が正しい答ですね。
式で書くと
$\large\frac{1}{4}$＋$\large\frac{2}{4}$＝$\large\frac{3}{4}$
となります。分母は変わらずに、分子だけを足し算していますね。
では、今度は引き算をしてみましょう。
$\large\frac{5}{7}$ー$\large\frac{2}{7}$＝？
$\large\frac{5}{7}$ （青の部分）
$\large\frac{2}{7}$ （緑の部分）
$\large\frac{?}{?}$ （茶色の部分）
青の部分から緑の部分を引くのですから、
上の数直線の茶色の部分の大きさが答になるのは分かりますね。
この茶色の部分を分数で表すとどうなりますか？
７等分したうちの３つ分になっていますね。
だから、それを分数で表すと、
$\large\frac{3}{7}$
になります。式で書くと、
$\large\frac{5}{7}$ー$\large\frac{2}{7}$＝$\large\frac{3}{7}$
となります。この２つの足し算・引き算の式を並べて書くと、
$\large\frac{1}{4}$＋$\large\frac{2}{4}$＝$\large\frac{3}{4}$
$\large\frac{5}{7}$ー$\large\frac{2}{7}$＝$\large\frac{3}{7}$
この２つの式を見れば分かるように、分母の数は変わりません。
分子の数だけを足したり引いたりして答えを出しています。
次の計算も同じやりかたでやってみましょう・・・。
$\large\frac{2}{4}$＋$\large\frac{3}{4}$＝$\large\frac{5}{4}$
お、こんどは分子の数が分母より大きくなりましたね。
これはどんな分数なのでしょう？
この分数の意味は「４等分したうちの５つ分」ということですから、
え？ ４つに分けたのに、４つより多い数って、ありえな～い！
と言いたくなるかもしれません。
でも、これも数直線で考えると、理解できますよ。
$\large\frac{2}{4}$ （青の部分）
$\large\frac{3}{4}$ （緑の部分）
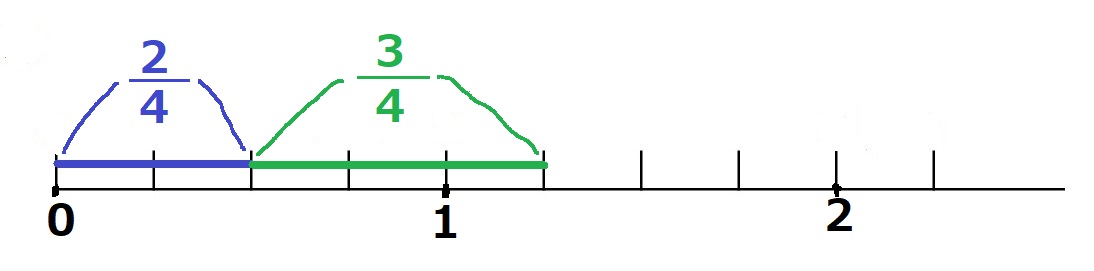$\large\frac{5}{4}$ （青と緑の部分）
今まで出てきた分数は、みんな１より小さい数だったけど、
１より大きい数も分数で表せるんだね。
１より大きいか小さいかを見きわめる方法は分かるかな？
そう、分子の数と分母の数を比べると分かるね。
分母と分子の数が同じなら、どんな分数も１と等しい（同じ）
分子の数が分母の数より小さければ、１より小さい
分子の数が分母の数より大きければ、１より大きい
ということが言えるね。
次は、前回の復習をかねて、次の計算をしてみましょう
１ー$\large\frac{2}{5}$＝$\large\frac{?}{?}$
前回で、「分母と分子が同じ分数は、すべて１になる」ということを学びました。
１ のままだと、計算が出来ないけど、
１ は $\large\frac{5}{5}$ と同じだから、１の代わりに $\large\frac{5}{5}$ を使えば、計算が出来ますね。
式で書くと、次のようになります。
１ー$\large\frac{2}{5}$＝$\large\frac{5}{5}$ー$\large\frac{2}{5}$＝$\large\frac{3}{5}$
今回は、分数の足し算・引き算の学習でした。
前回と今回（６，７）で学んだことがよく分かっているか、以下のリンク先問題でチェックしてみましょう。
教育出版 花まるワーク 分数３年
東京書籍 算数うでだめシート 分数３年
最後まで読んでくださり、ありがとうございました。
以下のボタンによるシェア、コメント欄・お問い合わせからのご意見・ご感想などをいただけると嬉しいです。今後ともどうぞよろしくお願いいたします。
