◎3種類の分数
4年生では、下に書いてあるように、分数には3つの種類があるということを学びます。
・真分数(しんぶんすう)
・仮分数(かぶんすう)
・帯分数(たいぶんすう)
今回は、それぞれがどんな分数のことなのかを学びます。
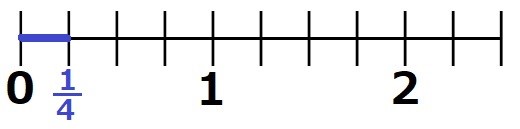

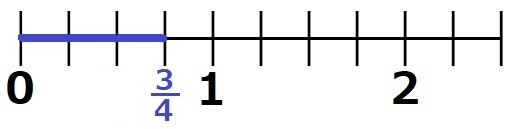
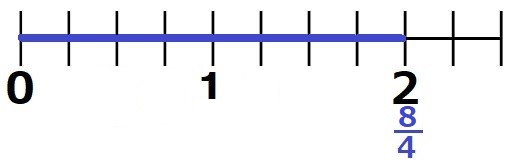
ここまでが真分数(分子が分母より小さい分数)
これより大きい分数が仮分数(分子が分母と同じか、分母より大きい分数)

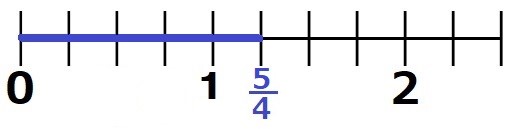



真分数(しんぶんすう)とは、
分子と分母を比べた時に、分子が分母より小さい分数のことです。
仮分数(かぶんすう)とは、
分子が、分母と同じか、分母より大きい分数のことです。
ここで問題です。
仮分数の
$\large\frac{5}{4}$
は1よりも大きいですか? 大きいとしたら、どのくらい大きいですか?
上の線分図からも分かる通り
1=$\large\frac{4}{4}$
ですから、
$\large\frac{5}{4}$
と比べると、1($\large\frac{4}{4}$)よりも
$\large\frac{1}{4}$
だけ大きいですね。ですから、
$\large\frac{5}{4}$=1+$\large\frac{1}{4}$
と書くことが出来ます。
1+$\large\frac{1}{4}$
のことを
1$\large\frac{1}{4}$
と書いて「1と4ぶんの1」と読みます。
このように、整数と真分数に分けて書いた分数のことを
帯分数(たいぶんすう)
といいます。
今度は
$\large\frac{11}{5}$
という仮分数を帯分数になおしてみましょう。
数直線で考えると分かりやすいですね。
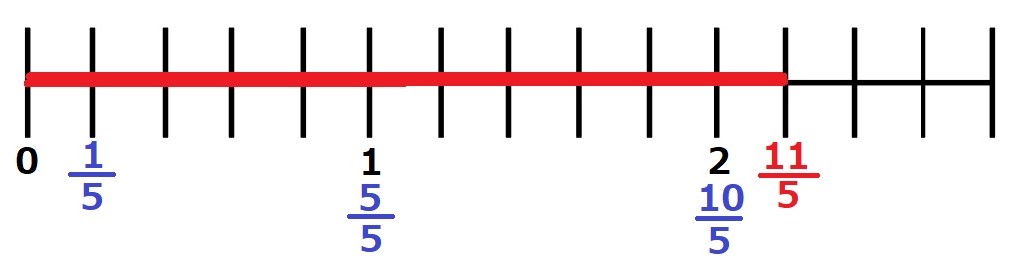
$\large\frac{11}{5}$ は $\large\frac{1}{5}$ を11こ集めた数です。
ということは、$\large\frac{5}{5}$ が2つと $\large\frac{1}{5}$ のことでもあります。
$\large\frac{5}{5}$ というのは1のことですから、
1が2つと $\large\frac{1}{5}$
ということになるので、
$\large\frac{11}{5}$=2$\large\frac{1}{5}$
と書くことができます。
なぜ仮分数を帯分数になおすかというと、
$\large\frac{11}{5}$
のままでは、その大きさがどのくらいなのか(2より大きいのか、3と比べるとどうなのか・・・)、すぐには分かりにくいけど、
2$\large\frac{1}{5}$
という帯分数なら2より $\large\frac{1}{5}$ だけ大きい数というように、その大きさが分かりやすくなるからです。
次は、
$\large\frac{13}{4}$
を帯分数になおしてみましょう
今度は数直線を使わずに、計算でやってみましょう。
考え方としては、
・その仮分数の中に1がいくつあるかということをまず考えます。
その結果が帯分数の整数部分になり、
・その残りが分数部分になります。
1がいくつあるかを見つける方法は、
仮分数の分母の数を使います。
なぜなら、
$\large\frac{13}{4}$
という仮分数の場合、分母と分子を同じにした分数の
$\large\frac{4}{4}$
を1のかわりに使って計算すると分かりやすいからです。
$\large\frac{13}{4}$
の中に
$\large\frac{4}{4}$
がいくつあるを見つけるには、分子の13の中に4がいくつあるかが分かれば良いので、
13÷4
を計算して、商(割り算の答)が3、余りが1なので、
$\large\frac{13}{4}$ = 3 + $\large\frac{1}{4}$ = 3$\large\frac{1}{4}$
となります。
この結果から、
$\large\frac{13}{4}$
は、3より $\large\frac{1}{4}$ だけ大きい数、ということが分かります。
「仮分数を帯分数になおすときは、分子を分母でわったときの、商とあまりをつかえばよいということですね」
ここでは、
真分数、仮分数、帯分数という言葉の意味とその使い分けをしっかりと身につけておく必要があります。
この言葉の覚え方ですが、
「真」という言葉には「本当の」という意味があり、
分子が分母より小さい分数は、最初に習った分数でもあり、
$\large\frac{3}{5}$
なら、「5つに分けた内の3つ分」
というように、その大きさが分かりやすい分数なので、
こういう分かりやすい形の(分子の数が分母の数より小さい)分数のことを
「真分数」と呼んでいます。
また、「仮分数」というのは「仮(かり)の分数」という意味で、
本当の姿は別にあるのだけど、都合があって、仮の姿になっている
ということです。
この都合というのは、後々分かってきますが、計算をより簡単にするために仮分数を使うということです。
では、本当の姿は何かというと「真分数」のことですが、仮分数は1以上の分数のことですから、「真分数」だけでは、表すことが出来ません。
そこで、「整数」と「真分数」を並べて書く「帯分数」が使われるわけです。
「帯分数」の「帯」という言葉には「手を取り合う」という意味があり、「連帯」という熟語などでもその意味が使われています。
「整数」と「真分数」が並んで手を取り合っている様子から、この「帯分数」という言葉が使われることになったと思われます。
「1より大きい分数は、仮分数と帯分数の2つの表し方がある」ということですね。
少し長くなりましたので、続きは次回にいたしましょう。
今回は、「3種類の分数:真分数・仮分数・帯分数」についての学習でした。
次回もこの続きを学びますので、この言葉の意味をよく理解して、特に仮分数・帯分数という言葉を自分でも使えるようにしておきましょう。
今回学んだことが身に着いているか、
ラビちゃんの算数プリント4年
の「(38)分数の表し方」
の問題で確認しておきましょう。
最後まで読んでくださり、ありがとうございました。
以下のボタンによるシェアや、コメント欄・お問い合わせからのご意見・ご感想などをいただけると嬉しいです。今後ともどうぞよろしくお願いいたします。